1. 子集构造(Subset Construction)
这是一个转换NFA到DFA的算法。我们知道NFA和DFA的区别最主要的就是一个状态和一个input symbol是否能够确定一个状态的问题,对于NFA,它将确定一个组状态,而DFA将确定一个状态,因此,我们有一个很好的办法就是把NFA的状态集对应每个DFA的状态,这就是subset construction的思想,不过这只是大概泛泛而论,我们需要更加明确的认识
1) NFA在任何一个input symbol下,映射的状态集(通过move函数,这个集合通常用T字母表示)应该被知道
2) 必须保证1)中状态集都对应了DFA中的一个状态
具体算法:
Input : 一个NFA N
Output : 接受相同语言的DFA D
Method : 为D构架一个transition table(转换表) Dtran,每个DFA的状态是一个NFA的状态集合(这里一定要注意前面说过的1)2)两点)。我们定义一些操作:
s 表示NFA的状态,T 表示NFA的状态集合,a表示一个input symbol
ε-transition(ε转换)就是说input symbol为ε时的transition(转换)
操作(operation) | 描述(description) |
ε-closure(s) | 从NFA的状态s出发,只通过ε-transition到达的NFA的状态集合 |
ε-closure(T) | NFA的集合T中的状态p,只通过ε-transition到达的NFA的状态集合,再求这些集合的交集。用数学表达就是 {p|p 属于 ε-closure(t) , t属于T} |
move(T,a) | NFA的集合,这个集合在input symbol为a,状态为T中任意状态情况下,通过一个转换得到的集合 |
注意一下,所有的操作都是针对NFA的状态或者状态集合,得到的时NFA的状态集合,或者说是DFA看为一个状态
Subset Construction
初始Dstates,它仅仅含有状态(D的状态)ε-closure(s0),并且状态未被标记,s0表示开始状态,注意,Dstates放的是D的状态
while ( Dstates 有未标记的状态 T ) { // T是D中的一个状态,也是N中一个状态集
标记 T;
for ( input symbol a ){ // 遍历所有的input symbol
U = ε-closure(move(T, a)); // move为NFA的move函数
if ( U 不在 Dstates 中 )
把U作为尚未标记的状态加入Dstates;
Dtran[T, a] = U
}
}
注意,状态s,ε-closure(s)一定包含s
我们先来熟悉上面的操作operation,再来看上面的算法
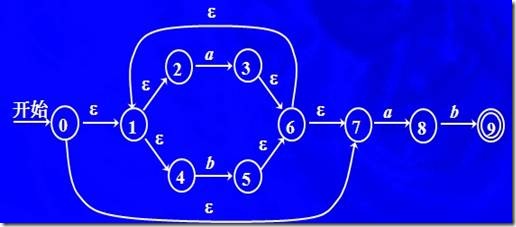
ε-closure(0) = {0, 1, 2, 4, 7} // 从0状态出发的,input symbol为ε的所有状态的集合
ε-closure(3) = {1, 2, 3, 4, 6, 7}
ε-closure(8) = {8}
ε-closure( {3, 8} ) = ε-closure(3) U ε-closure(8) = {1, 2, 3, 4, 6, 7, 8}
move(0,a) = 空
move(7,a) = {8}
move(8,b) = {9}
move( {0, 1, 2, 4, 7}, a) = move(0,a) U move(1,a) U move(2,a) U move(4,a) U move(7,a) = {3, 8}
现在可以回去理解一下算法了。
这里再说说求ε-closure(T)的算法:
把T的所有状态压入stack(栈);
ε-closure(T)的初始值为 T 中的所有元素 ; // 也就是一定包含他们本身
while( 栈非空 ) {
弹出栈顶元素 t ;
for( 每个属于 move(t, ε) 的状态 u ){
if( u 不在 ε-closure(T) 中 ){
u 加入 ε-closure(T);
把 u 入栈;
}
}
}
下面对上图如何使用Set Construction算法来构建DFA做一个详细的描述:
1. 初始化Dstates 把集合 ε-closure(s0) = {0, 1, 2, 4, 7}作为第一个状态,设此状态为 A
2. 现在转化,input symbol {a, b},因此,求:
ε-closure(move(A, a));
ε-clo�sure(move(A, b));
这里会得到2个状态
ε-closure(move(A, a)) = {1, 2, 3, 4, 6, 7, 8},设其为 B
ε-closure(move(A, b)) = {1, 2, 4, 5, 6, 7}, 设其为C
B,C放入Dstates
改写 Dtrans
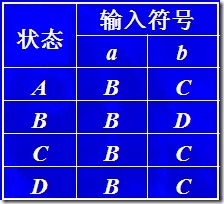
最终得到的 Dtrans 为:
A = {0, 1, 2, 4, 7}
B = {1, 2, 3, 4, 6, 7, 8}
C = {1, 2, 4, 5, 6, 7}
D = {1, 2, 4, 5, 6, 7, 9}
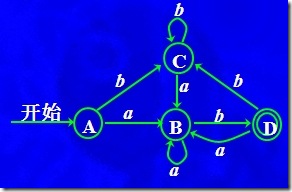
因此,NFA转化成为DFA:
编缉推荐阅读以下文章
版权与免责声明
1、本站所发布的文章仅供技术交流参考,本站不主张将其做为决策的依据,浏览者可自愿选择采信与否,本站不对因采信这些信息所产生的任何问题负责。
2、本站部分文章来源于网络,其版权为原权利人所有。由于来源之故,有的文章未能获得作者姓名,署“未知”或“佚名”。对于这些文章,有知悉作者姓名的请告知本站,以便及时署名。如果作者要求删除,我们将予以删除。除此之外本站不再承担其它责任。
3、本站部分文章来源于本站原创,本站拥有所有权利。
4、如对本站发布的信息有异议,请联系我们,经本站确认后,将在三个工作日内做出修改或删除处理。
请参阅权责声明!