在说到这个问题前，先告诉大家，我们可以直接从 Regular expression 到 DFA，不过这里我们先不讨论这个问题

　　关于RE到DFA的算法有很多，这里学习一个最简单的

　　Algorithm Thompson's construction：

　　Input : 一个字母表(Σ)上的 Regular Experssion r

　　Output : 一个接受 L(r) 的 NFA N

　　Method : 把 r 解析成为子表达式(subexpressions)，然后使用下面的1),2)规则，为 r 中的基本符号(basic symbols,基本符号就是ε和Σ中的字符)构建NFA，基本符号符合1),2)关于正规式的定义，注意，假如symbol a 出现多次，那么它每次出现都要构建一个NFA。之后，我们需要通过 r 的语法结构，通过规则3)组合前面构建的NFA，直到得到整个NFA为止。对于中间产生的NFA，它只有一个终态，没有进入开始装状态的边，也没有离开接受状态的边。

　　1) 对于 ε 构造如下NFA

　　注意，每次构建时，i,f的值都不一样，因此可见构造一个识别 ε 的NFA，会产生2个新的状态

　　2) 对于Σ中的每个字符a

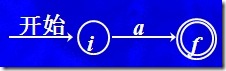
　　同样，对于aaa，第一个a构造的NFA中的i,f不会和第2个a构造的i,f一样，因此可见构造一个识别Σ中的每个字符a 的NFA，会产生2个新的状态

　　3) 先假定 N(t) N(s) 分别是 t s 的NFA，则：

　　a) 对于表达式 s|t 构建 NFA N(s|t)

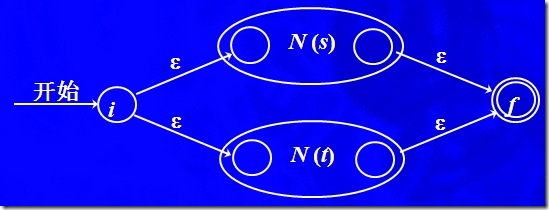
　　这里一样会产生2个新的状态i,j，我们看其中一个N(s)，左边的圆圈，表示N(s)的开始状态，右边的圆圈表示N(s)的接受状态，N(t)同理

　　b) 对于表达式 st ,构建N(st)

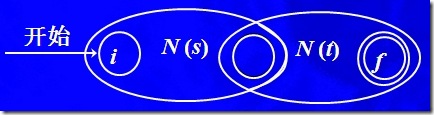
　　这个时候，不产生新的状态，N(s)的开始状态变为N(st)的开始状态，N(t)的接受状态变成N(st)的接受状态，N(s)的接受状态和N(t)开始状态成为一个状态。这里提醒一下，写程序的时候，这里千万要注意，因为没有新的状态产生，必须考虑状态的部分复制，如果不小心就会出错。

　　c) 对于正规式 s*，构造N(s*)

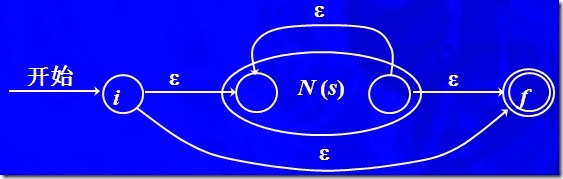
　　这里一样需要产生2个新的状态i,f，注意，产生了一条N(s)接受状态到N(s)开始状态的边，边上的symbol为 ε

　　d) 对于(s)，使用N(s)本身作为它的NFA，也就是不用构造新的NFA

　　注意一下，以上产生的NFA，有以下性质：

　　1) 只有一个接受状态和一个开始状态

　　2) 每个状态最多含有2个指向其他状态的边，详细的来说，如果状态只有一条指向其他状态的边，那么边上的symbol为Σ中的任意字符或者ε，如果状态有两条指向其他状态的边，那么边上的symbol一定为2个ε

　　由以上性质，我们可以很好的选择数据结构来表示NFA

编缉推荐阅读以下文章

• 词法分析(6)---DFA的化简
• 词法分析(4)---NFA与DFA的转化
• 词法分析(3)---DFA
• 词法分析(2)---NFA
• 词法分析(1)---词法分析的有关概念以及转换图
• 一个小语言的词法分析程序